Partimos del siguiente sistema de ecuaciones
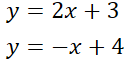
Lo ordenamos. Para ello, ponemos todas las incognitas en el primer miembro y dejamos los números solos, en el segundo miembro. En este caso, las x están en el miembro o lado derecho y las tenemos que pasar a la izquierdo. No obstante, los números solos, si ya se encuentran en el lado derecho y por ello, no tenemos la necesidad de cambiarlos. . Quedarían así las nuevas ecuaciones
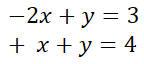
Por una cuestión de costumbre escribo primero a las x y luego a las y. Pero, esto no es obligatorio. Lo que si es obligatorio es que las x y las y en ambas ecuaciones tienen que estar encolumnadas, tal como se ilustra en la siguiente imagen
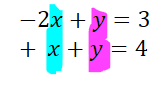
Una aclaración a tener en cuenta, cuando las incógnitas no presentan un coeficiente expreso, se entiende que tienen tacitamente a 1 como coeficiente. En este caso, el sistema se podría escribir así y resultaría igual al anterior
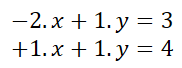
Ahora se preparan 3 determinantes. Que los llamaremos
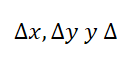
Para el primer determinante, se colocan los escalares, los resultados, en la primer columna. Y, los coeficientes de las y, en la segunda.
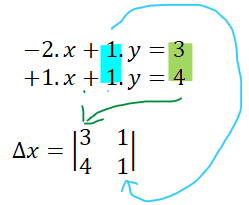
Para el segundo determinante, se colocan los escalares, o sea los resultados, en la segunda columna. Y, los coeficientes de las x, en la primera.
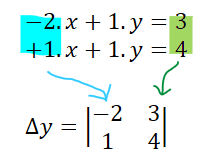
Y, el tercer determinante se confecciona así.
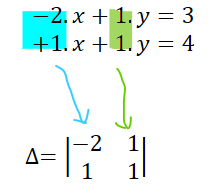
Ya contamos con los 3 determinantes. Y procedemos a calcularlos
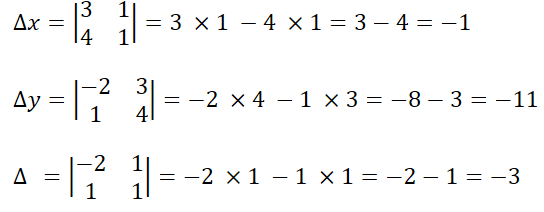
Luego, calculamos las respuestas, mediantes los cocientes.
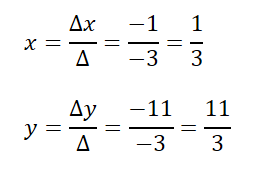
Siendo las respuestas x = 1/3 e y = 11/3
La verificación, no es un paso obligado. Pero, si es un paso útil. Primero porque aclara si el ejercicio está resuelto. Y, segundo tiempo porque en sí, la verificación enseña. Para ello, se reemplaza en las 2 ecuaciones los datos obtenidos.
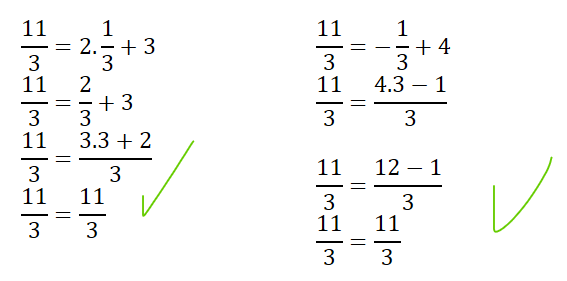
Observando que ambas ecuaciones quedan igualadas. Quedando el ejercició concluido.



